Hi All! Today I thought of writing about some research work that I did as part of my PhD which is an intersection between machine learning and anomaly detection. In a nutshell an anomaly is a novel pattern in a dataset that was never observed before or a pattern that is rarely seen. Identifying anomalies in data has a lot of important use cases. For example consider the case of an ECG reading of a heart patient. Automatically identifying anomalous patterns can greatly help doctors diagnose illnesses effectively and efficiently, there by increasing the chance of saving lives. In the recent past Machine learning and AI have been successfully used in many scenarios for anomaly detection. In this piece of work we develop a model called RAMP short of Real-Time Aggregated Matrix Profile that is able to identify anomalous patterns in a multivariate time series (i.e., a time series with many features) in an online real-time manner.
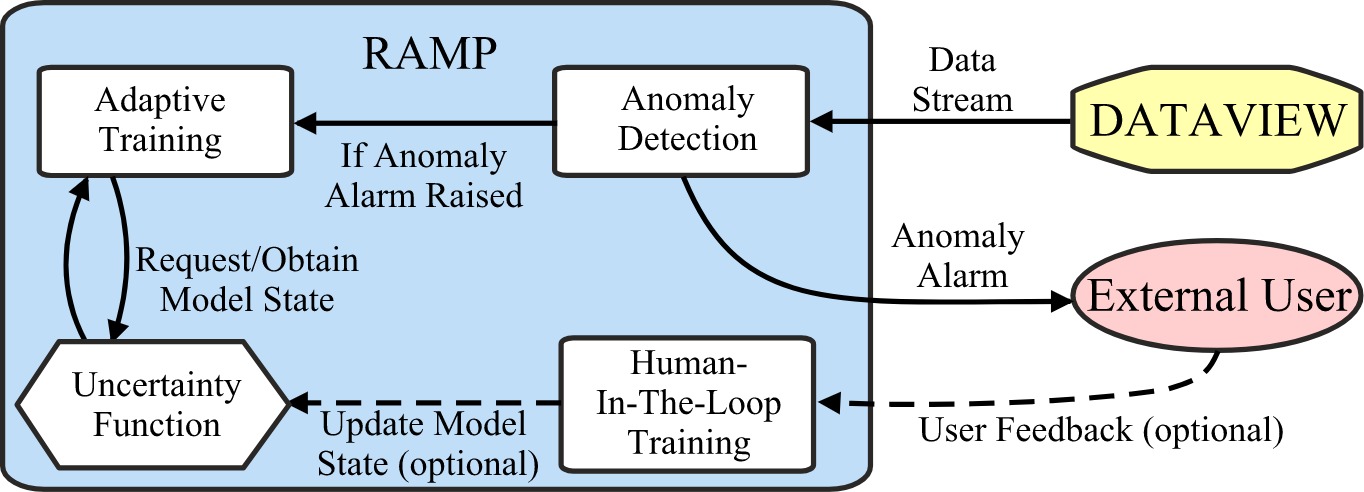
The image above is the architecture of RAMP. RAMP is designed for applications where the data forms a time series stream, meaning there is a continues flow of data. Streaming data poses an additional challenge for machine learning based anomaly detection models. Usually in machine learning, models generalize patterns in data based on pre-collected training datasets by training on them offline (e.g., most deep learning models). Usually, this offline training process requires substantial amount of time and computational resources. However, in streaming data, the data arrives continuously and patterns are bound to continuously change meaning that models must learn temporal behavior in an online manner on the fly. So that was our challenge, we had to make sure our model is fast enough to keep up with the stream of data while ensuring it can still learn complex temporal patterns and identify anomalies at the same time. In today’s’ post I will be going through a brief overview of RAMPs’ features and its key ideas along with an implementation in python. Full disclosure, this post itself might not be sufficient to completely understand all the inner working of RAMP, rather what I wanted to write about was why we designed RAMP in this way and the challenges it overcomes. If you want more in depth information about our model please refer to the code, paper or slides.
We experimented RAMP on streaming system logs collected from DATAVIEW, a scientific workflow management system used for conducting large scale experiments with the aid of Amazon EC2 virtual machines (e.g., forecasting earthquakes, diagnosing illnesses). By using RAMP we showed that it is possible to identify a variety of anomalies in such systems and possible malicious activity that may have been carried out to falsify research. We selected such a domain because falsified research findings can have serious implications in many areas. For example imagine if fraudulent research was used for drug discovery for some disease, then it could have serious side effects for any patient that use those drugs. Or imagine a governmental policy decision was carried unknowingly based on some falsified research, this again could have serious negative implications on the society at large. Therefore, ensuring that research is credible and reproducible is of great importance in the research community [1,2]. On another note, scientific workflows run on dedicated machines and hardware. Therefore, capturing anomalies in those systems as they occur is of paramount importance to not waste precious computational resources. The system logs form a multivariate time series that reflects the current execution state of any given experiment on the Amazon machines. In the GitHub code, I have also provided an example of how RAMP works for a simple dataset collected on DATAVIEW. As shown in the image RAMP continuously monitors the stream of data and gives an indication of an anomaly to the user. As shown in the image above RAMP works as follows:
- Identifies potential anomalies in the streaming data using the Anomaly Detection module
Ifan anomaly flag is raised: undergoes one training cycle using Adaptive Training module using the Uncertainty Function (Note: no human feedback is given)- Optionally can undergo an additional training cycle if human feedback is given using Human-In-The-Loop Training (to rectify any errors made by RAMP)
1. Anomaly Detection
We built the Anomaly Detection module by improving on an existing time series analysis model called the Matrix Profile (super stoked and humbled that our work is also featured in the original MP page :) ). Basically, the idea behind Matrix Profile is quite intuitive. Given a time series, the model breaks it into small subsequences of some predefined small length before operating on them. For example, assume a uni-variate time series with 50 data points \(T= \{t_1, t_2, ..., t_{50} \}\) and the subsequence length \(m = 3\), then the first subsequence will be \(\{t_1,t_2,t_3\}\) and the final subsequence being \(\{t_{48}, t_{49}, t_{50} \}\). Then the set of all subsequences are \(\{ \{t_1, t_2, t_3 \}, \{t_2, t_3, t_4 \}, ..., \{t_{48}, t_{49}, t_{50} \} \}\). The Matrix Profile (MP) works as follows:
For each subsequence:
(1) Compute distance between current subsequence and the entire subsequence set
(2) Find the minimum from the above computed distance excluding distance to itself
(3) Append the identified min-distance as the MP value for current subsequence
For some subsequence, if the MP value is zero or a very small value then it means that subsequence is a common pattern that occurs within the times’ series. If the MP value is very large that means the pattern in question is an outlier or an anomaly. In our anomaly detection algorithm, we extend and modify the vanilla Matrix Profile approach to work with a streaming multivariate data source. I won’t go into our exact modifications here, instead I will refer you to the slides or the paper for more information. Our anomaly detection algorithm, takes each oncoming subsequence as its input and computes a weighted aggregated anomaly score \(\beta\). If this anomaly score is greater than some user defined threshold (\(\beta > \theta\)) then it returns True for anomaly. Additionally, given a multivariate time series, our algorithm also returns the features that contributed towards an identified anomaly instance. Thereby some user or administrator will be able to diagnose the root cause of an anomaly.
def anomaly_detection(self,t,T,proc_id=0):
""" identifies if an anomaly is present in sub-sequence T """
""" ----------------------- """
""" @param t : the time step [0,...,M-1] within the window M """
""" @param T : a multi-dimensional subsequence [d,m] """
""" @param proc_id : the id of the process if experiment is interleaved, 0 is default """
""" ----------------------- """
""" @return [anomaly_detected,beta,C_t] """
beta = 0 """ anomaly score """
key = 0 """ index of the weight dictionary """
C_t = np.zeros(self.d) """ contribution to beta from all features/dimensions """
D_min = np.zeros(self.d) """ an empty list to store min(Distance-value) for each d """
""" computing the relative distance for each dimension/feature """
for j in range(self.d):
min_rd = np.inf """ initially has infinite relative distance """
min_k = -1 """ a temp variable for computing the index of the weight """
for k in range(self.M - self.m):
abs_distance = np.sum(np.abs(np.subtract(T[j],self.T_[proc_id,j,k:k+self.m])))
compared_with = np.sum(np.abs(self.T_[proc_id,j,k:k+self.m]))
relative_distance = abs_distance / compared_with
if relative_distance < min_rd:
min_rd = relative_distance
min_k = k
self.R[proc_id,j,t] = min_k
key += ((self.M - self.m)**j)*min_k
beta += min_rd
D_min[j] = min_rd
""" -------------------- """
C_t = (np.divide(D_min,beta) if beta > 0 else np.zeros(self.d)) """ computing the contribution to the anomaly """
self.H[proc_id,t] = (beta / self.theta if beta > 0 else 1e-10) """ updating the ratio between (un weighted beta/theta) """
""" computing the weighted score """
if int(key) in self.W[proc_id]:
beta = self.W[proc_id][int(key)] * beta
""" get anomaly flag """
if beta > self.theta:
return [True,beta,C_t]
else:
return [False,beta,C_t]
2. Adaptive Training
Whenever a possible anomaly is identified, RAMP undergoes one training cycle. This training cycle is needed to reduce the False Positives identified. In our training algorithm the weights used to compute the anomaly score are modified.
The biggest question of anomaly detection is, how can a model decide if an anomaly flag (i.e. True for anomaly) is actually some malicious activity or that it signifies something wrong instead of it have being a false alarm, without any human intervention?.
To answer this question we gave RAMP the ability to guess. We defined a novel feature called the uncertainty function that gives a probabilistic value \(p\) (i.e., between 0 and 1) that indicates whether RAMP should consider the anomaly instance as a True Positive or a False Alarm. The training algorithm biases the degree to which the weights are modified depending on the value of \(p\).
def uncertainty_function(self,proc_time,proc_id=0):
""" gives a probabilistic value for the uncertainty of whether an anomaly flagged is TP or FP """
""" ----------------------- """
""" @param proc_time : the time with respect to the individual process [0,...,inf] """
""" @param proc_id : the ID for the interleaved process, default = 0 """
""" ----------------------- """
""" @return probabilistic value [0,1], if ~1 then most likely TP """
if proc_time > self.M:
return np.abs(1 - np.exp(self.K[proc_id]**self.b - proc_time**self.b))
else:
return 0
def adaptive_training(self,t,p,proc_id=0):
"""conducts one training cycle, does not return because W,H are defined in class"""
""" ----------------------- """
""" @param t: time step [0,...,M-1] within the range M """
""" @param p: the result from the uncertainty function """
""" @param proc_id : the process id, default = 0 for only one process """
keys = np.zeros(2*self.m+1) """ the indices of the weights to train """
for k in range(2*self.m+1):
""" compute the index for the weights """
for j in range(self.d):
keys[k] += ((self.M-self.m)**j)*(self.R[proc_id,j,t] - self.m + k)
""" add weight into W, if it does not exist in W """
if keys[k] not in self.W[proc_id]:
self.W[proc_id][keys[k]] = 1
""" weight updating step """
if k == self.m :
beta_unweighted = (self.H[proc_id,t] * self.theta) / self.W[proc_id][keys[k]]
self.W[proc_id][keys[k]] *= ( (self.alpha[k]*(1-p)) / (2*self.H[proc_id,t]) )
self.H[proc_id,t] = (self.W[proc_id][keys[k]] * beta_unweighted) / self.theta
else:
self.W[proc_id][keys[k]] *= ( (self.alpha[k]*(1-p)) / (2*self.H[proc_id,t]) )
return
3. Human-in-the-loop Training
Even though RAMP can guess and trains its own parameters there might be instances where the guess itself is wrong. In those instances RAMP needs some external input to rectify any mistake. From a models point of view, the most sure proof way of obtaining external input is from some human operator. Therefore, we also develop an optional Human-In-The-Loop training module. This component has two functionalities - (1) to rectify any unwanted training resulting because RAMP may have mistakenly modified weights of a true positive anomaly instance thinking it’s a false alarm and (2) updating the parameters of the uncertainty function based on the number of false alarms reported by RAMP in the recent past. However, it should be noted that this is an optional component and it’s entirely possible to run RAMP without it.
def human_in_the_loop_training(self,proc_time,num_fp,U_TP,proc_id=0):
""" optional periodic training, if user feedback is given, does not return """
""" because K,W are defined in class """
""" ----------------------- """
""" @param proc_time : the time index for the current process [0,..,inf] """
""" @param num_fp : the total number of false positives marked """
""" @param U_TP : the indices for the True Positives [0,..,M-1] """
""" @param proc_id : the process id, default = 0 """
""" update step for the uncertainty function parameter """
self.K[proc_id] += (proc_time - self.K[proc_id])*(num_fp/self.M)
""" weight update step for True Positives """
for i in U_TP:
key = 0 """ the index of the weight """
for j in range(self.d):
key += ((self.M-self.m)**j)*self.R[proc_id,j,i]
if key not in self.W[proc_id]:
self.W[proc_id][int(key)] = 1
self.W[proc_id][int(key)] *= (2/self.H[proc_id,i])
return
There you have it, my first ever anomaly detection model RAMP. If you find it interesting please do read the paper, slides and play with the code.
So until next time,
Cheers!
Next: Anomaly detection with Deep AutoEncoders
Prev: Time series prediction with Recurrent Neural Networks (RNNs)