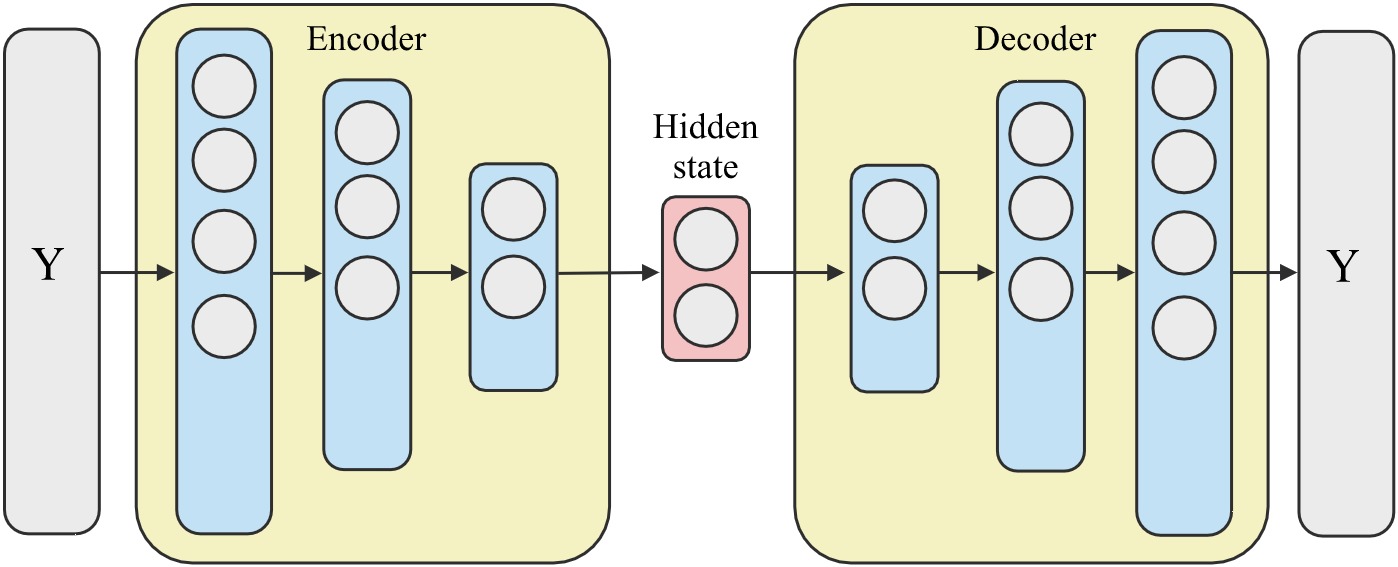
Today I will be writing about another deep learning model named an AutoEncoder. As shown in the image above, an AutoEncoder model has two main components–1) an Encoder module and a 2) Decoder module. The Encoder is given some tensor input, named as Y in this case, and it learns some hidden representation of it usually called a hidden state. The Decoder in turn obtains this hidden state tensor and learns to reconstruct the original input Y. Given that, a trained model is able to recreate Y with minimum error, then it stands to reason that the hidden state is in fact some compact representation of the original input Y. Typically, it’s possible to obtain a hidden size that is much smaller with respect to the original tensor Y.
As such, AutoEncoders have been used extensively to handle the curse of dimensionality problem in Machine Learning. But in the post today, I will be focusing on the use of AutoEncoders as anomaly detection models while providing a skeleton code of a feed forwarding neural network based implementation using the Pytorch framework. I have divided the implementation into two sections. First an AutoEncoder Module which represents the construction of the neural network and then training and the anomaly detection process.
1. The AutoEncoder Module
Given that we have some data, an anomaly is a data point that is considered as a outlier sample. Outliers don’t really appear much in a given dataset, so from a supervised machine learning point of view outlier detection or anomaly detection can be a hard task. Because, typically supervised machine learning tasks work best when we have an equal distribution in the classes (i.e., benign class and the anomaly class). But as per the definition of anomalies, we won’t really see anomaly data points in a data set as much as we see normal behaviour. This being the case its possible to use AutoEncoder models in a semi-supervised manner in order to use the model for anomaly detection. This involves two steps:
- First the AutoEncoder model is trained on the benign class alone. Then a trained AutoEncoder will be able to accurately reconstruct any data sample from the
normalclass. The reconstruction error or loss of the model can be used as an anomaly score. Since the reconstruction of a benign class sample must be accurate, then the anomaly score would be low. - During deployment, whenever the AutoEncoder encounters an anomaly sample, it would not be able to recreate the anomaly sample accurately. This would result in a large reconstruction error for this specific data sample. Whenever this anomaly score is high, it’s likely that the encountered data sample is an anomaly. When its low, then its most likely a normal data point.
The following AutoEncoderModule python class gives an implementation using feed forwarding neural networks as the basis of the Encoder and the Decoder. Notice, that in the init() function I have defined two sequentially concatenated layers. The first Encoder component is a neural network that decreases in size starting from the original input dimension down to a hidden state size. Similarly, the Decoder is a neural network that increases in size starting from the hidden state size up to the dimensions of the original input. This is a typical implementation of an AutoEncoder-Module, depending on the type of data you are working on it is possible to use LSTM/GRU for the Encoder/Decoder if its time series data or a CNN/GNN if its image data or graphs. The forward() function gives both the reconstructed input and the hidden state.
import torch
from torch.utils.data import DataLoader
from torch.autograd import Variable
import pandas as pd
import numpy as np
class AutoEncoderModule(torch.nn.Module):
""" the pytorch Neural Network module of the AutoEncoder """
""" The current implementation uses a feed forwarding neural network """
""" as the encoder and the decoder """
def __init__(self, input_dim, hidden_size, device):
""" init function"""
""" @param input_dim: the input dimension of the tensor """
""" @param hidden_size: the dimension of the hidden size """
""" @param device: cpu or gpu device to run in """
super(AutoEncoderModule, self).__init__()
self.input_dim = input_dim
self.hidden_size = hidden_size
self.device = device
""" define the encoder/ decoder layer steps """
dec_steps = 2 ** np.arange(max(np.ceil(np.log2(hidden_size)), 2), np.log2(input_dim))
dec_setup = np.concatenate([[hidden_size], dec_steps.repeat(2), [input_dim]])
enc_setup = dec_setup[::-1]
""" encoder definition """
layers = np.array([[torch.nn.Linear(int(a), int(b), bias = True)] for a, b in enc_setup.reshape(-1, 2)]).flatten()[:-1]
self._encoder = torch.nn.Sequential(*layers)
self.to_device(self._encoder)
""" decoder definition """
layers = np.array([[torch.nn.Linear(int(a), int(b), bias = True)] for a, b in dec_setup.reshape(-1, 2)]).flatten()[1:]
self._decoder = torch.nn.Sequential(*layers)
self.to_device(self._decoder)
return
def forward(self, ts_batch):
""" forward pass """
""" @param ts_batch: the batch of input tensors """
""" @returns reconstructed_sequence and the hidden_state (enc) """
flattened_sequence = ts_batch.view(ts_batch.size(0), -1)
enc = self._encoder(flattened_sequence.float())
dec = self._decoder(enc)
reconstructed_sequence = dec.view(ts_batch.size())
return reconstructed_sequence, enc
def to_device(self, module):
""" helper code to send to device """
module.to(self.device)
return
2. Training and Anomaly Detection
In the code below, I have used an instance of the above AutoEncoderModule and defined the training and anomaly detection tasks in the functions fit() and predict(). The initialization of the AutoEncoder is similar to a typical deep learning model with the parameters of batch size, learning rate, epochs to train and the device. The model specific parameters are the hidden size and the input dimension.
Notice, that in the init function, I have two variables for max_err and min_err. In practice, I usually prefer to normalize the reconstruction error within a specific range(i.e., [0,1]). This can be done by normalizing the reconstruction error within the minimum and maximum error values obtained during its training phase. Then during anomaly detection we can consider a sample to be an anomaly if the normalized reconstructed error (\(\beta\)) is greater than a given threshold (\(\theta\)).
As such, the fit() function does two tasks. First it trains the model for a given number of epochs on the training data. Afterwards it does one forward pass on the training data and identifies the minimum and maximum reconstruction loss. In this code example I have used the MSELoss for the training iterations and the L1Loss for anomaly detection. It’s possible to use other loss functions along with more complicated procedures to obtain the anomaly scores depending on the complexity of the application domain. The predict() function is quite straightforward. It basically does a forward pass on the data and computes anomaly scores. Unlike in the training phase we do not need to calculate the gradients, so using with torch.no_grad() usually saves time during this phase.
class AutoEncoder:
""" AutoEncoder model designed for anomaly detection """
""" uses the 'AutoEncoderModule' class """
def __init__(self, input_dim, hidden_size, batch_size, learning_rate=0.01, num_epochs=100, run_in_gpu=True):
""" init function"""
""" @param input_dim: the input dimensions """
""" @param hidden_size: hidden state size """
""" @param batch_size: batch size for single forward pass """
""" @param learning_rate: learning rate to train model """
""" @param num_epochs: the #iterations to train """
""" @param run_in_gpu: True if GPU is used """
""" AE model parameters """
self.input_dim = input_dim
self.hidden_size = hidden_size
self.device = torch.device("cpu")
if run_in_gpu:
self.device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
self.model = AutoEncoderModule(self.input_dim, self.hidden_size, self.device)
""" setting the training parameters """
self.lr = learning_rate
self.batch_size = batch_size
self.num_epochs = num_epochs
""" anomaly score normalizing constants """
self.max_err = None
self.min_err = None
return
def fit(self, X):
""" training the AutoEncoder model """
""" @param X: the training data """
""" (1) the training process """
X = torch.tensor(X, dtype=torch.float)
train_loader = DataLoader(dataset=X, batch_size=self.batch_size, drop_last=True, shuffle = True, pin_memory=True)
optimizer = torch.optim.Adam(self.model.parameters(), lr=self.lr)
for epoch in range(self.num_epochs):
for ts_batch in train_loader:
output, _ = self.model(self.to_var(ts_batch))
loss = torch.nn.MSELoss(reduction='sum')(output, self.to_var(ts_batch.float()))
self.model.zero_grad()
loss.backward()
optimizer.step()
""" (2) get error values to normalize anomaly score (optional) """
train_anomaly_loader = DataLoader(dataset=X, batch_size= X.shape[0])
with torch.no_grad():
for idx, ts in enumerate(train_anomaly_loader):
output, _ = self.model(self.to_var(ts))
error = torch.nn.L1Loss(reduction='none')(output,self.to_var(ts.float()))
error = torch.sum(error,1)
error = error.cpu().data.numpy()
self.min_err = np.min(error)
self.max_err = np.max(error)
return self.min_err, self.max_err
def predict(self, X):
""" complete pass for obtaining the anomaly score """
""" @param X: the test data """
X = torch.tensor(X, dtype=torch.float)
test_loader = DataLoader(dataset=X, batch_size= X.shape[0])
with torch.no_grad():
for idx, ts in enumerate(test_loader):
""" does one forward pass """
output, _ = self.model(self.to_var(ts))
error = torch.nn.L1Loss(reduction='none')(output, self.to_var(ts.float()))
error = torch.sum(error,1)
""" gets the anomaly score, normalized """
anomaly_scores = (error - self.min_err)/(self.max_err - self.min_err)
return anomaly_scores.cpu().data
def to_var(self, t, **kwargs):
t = t.to(self.device)
return Variable(t, **kwargs)
There you go, a speedy run through on how to code up an AutoEncoder model using Pytorch. Depending on your need its possible to use much more sophisticated neural network architectures and loss/error calculation metrics in AutoEncoders.
So until next time,
Cheers!
Next: Fooling AI-based System Log Anomaly Detection
Prev: RAMP: Real-Time Aggregated Matrix Profile